The calorimeter is a measuring device that aims to have an adiabatic process. The findings in this experiment are determined through the data gathered from a calorimeter. Thermocouples were placed in two locations to measure the temperature differences. The first law of thermodynamics proves that adiabatic assumption is when no heat or mass is lost to the surroundings of the system that is being analyzed. However, replicating such conditions is difficult to acquire without proper equipment. Therefore, the main purpose of the project was to account for the heat loss that occurs in the calorimeter. By analyzing the data presented in the sample, one must also determine uncertainties in the temperatures.
I begin this experiment by taking the mean from the two thermocouple readings (TCavgdata) and plotted onto a graph. The next step involves fitting a best fit line to the data. There are two regression lines that need to be found. First is the lower regression line, which is the pre-sample points that have an interval from the beginning of the data to the point where the sample is added. Next is the upper regression line that includes an interval from the highest temperature to the end of the data. Both regression lines can be calculated with linear least squares matrix method.
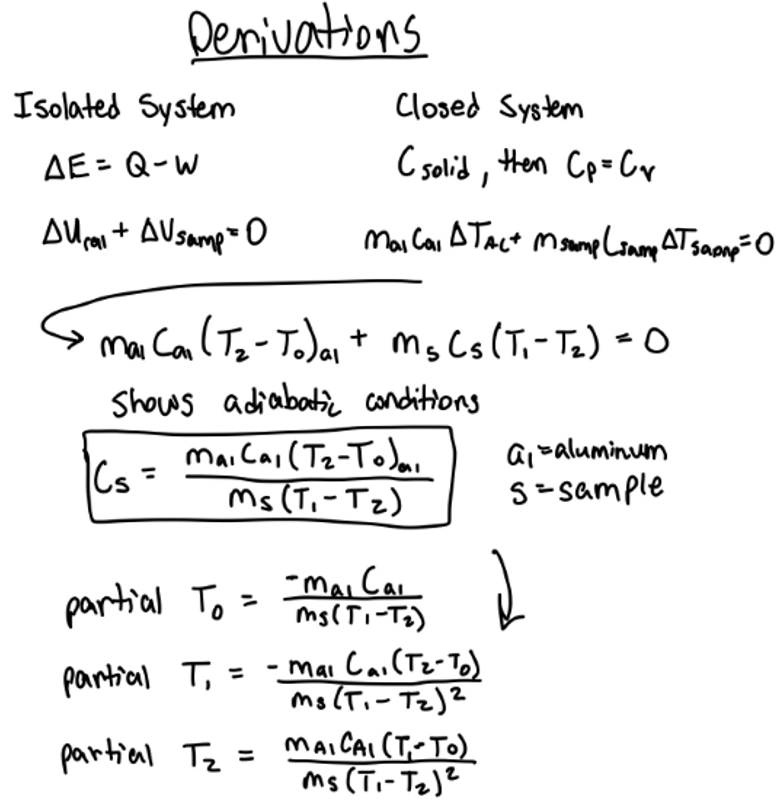
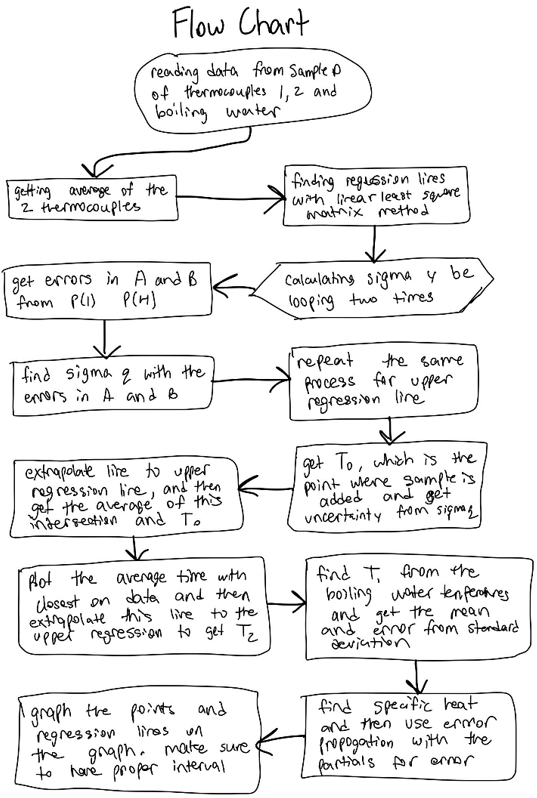
The initial temperature of the calorimeter (TLow = T0) and the final temperature at equilibrium (T2) can be determined by extrapolating regression lines. The initial temperature of the sample (T1) is found by taking the mean of the boiling water just before the temperature begins to drop. Finally, with specific heat of the calorimeter (Ca1), mass, and temperature, the specific heat of the sample (Cs) can be calculated.
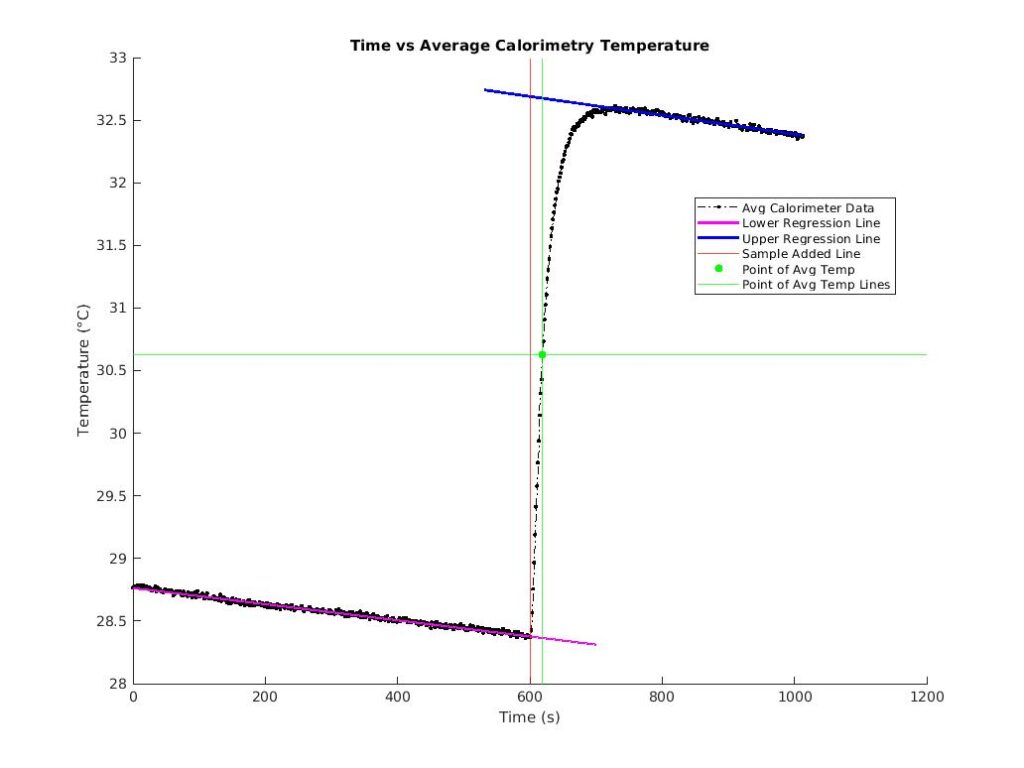
The red line helps us determine the values for the TLow (when it intersects with the lower regression line in purple) and THi (when it intersects with the upper regression line in blue). The light green line is the extrapolation of the average of the TLow and THi values, and when this line intersects with the upper regression line, we know T2.